ANÁLISIS VECTORIAL

Introducción al Análisis Vectorial

El estudio de los vectores que desarrollaremos nos ayudará a explicar, comprender y evaluar algunos fenómenos físicos que requieren para su descripción, del uso de magnitudes vectoriales como la velocidad de un avión, el desplazamiento de un automóvil, la fuerza aplicada a un ladrillo, la cantidad de movimiento de una bola de billar, etc.

Galileo Galilei (1564 – 1642) fue uno de los primeros científicos que al estudiar el movimiento de los proyectiles, tuvo la necesidad de usar vectores con el fin de determinar para un instante, la velocidad del proyectil, la composición de sus velocidades en la dirección horizontal y en la dirección vertical.

La importancia que tienen los vectores para la Física es que a través de ellos se representan las magnitudes vectoriales; lo cual permite una mejor descripción de los fenómenos físicos.

Las cantidades físicas por su forma geométrica o naturaleza pueden ser clasificadas como “escalares” o “vectoriales”.

Definición de Vector

Es un ente matemático que nos sirve para representar a las magnitudes de carácter vectorial. Se trata de segmentos de recta con orientación; si se dibujan a escala se representa la medida de la cantidad.

Para representar la dirección de las cantidades vectoriales se han ideado a los VECTORES.

Ejemplos: Desplazamiento, velocidad, fuerza, impulso, aceleración, campo eléctrico, etc.

Elementos de un Vector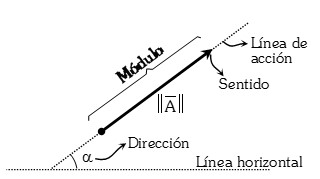

Módulo: Llamado también NORMA o TAMAÑO, es la medida de la longitud del vector, el módulo se representará mediante la notación:

Si un vector no aparece con flecha encima se sobreentiende que se refiere al módulo, como lo vimos anteriormente.

Dirección: Es el ángulo que forma el vector con respecto a un sistema de coordenadas cartesianas (por lo general se toma la orientación con respecto al semieje positivo de las abscisas).

Sentido: Representado por la flecha del vector.

Línea de Acción: Es aquella línea donde se encuentra contenido el vector a través de la cual puede deslizarse.

Representación Analítica de un Vector

Dados dos puntos A y B que determinan un vector sobre el plano, la forma vectorial se define por:

Clasificación de los Vectores

Vectores Colineales

Son aquellos que se encuentran contenidos en una misma línea de acción.

Vectores Iguales

Dos vectores serán iguales cuando tienen la misma dirección, módulo y sentido.

Vector Unitario

Es aquel cuyo módulo es la unidad y tiene por misión indicar la dirección y sentido de un determinado vector.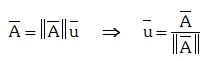

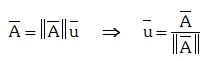
Vectores Paralelos

Son aquellos que tienen sus líneas de acción paralelas entre sí.

Vectores Coplanares

Son aquellos vectores que se encuentran contenidos en un mismo plano. 

Vectores opuestos

Dos vectores serán opuestos cuando tienen igual dirección, módulo pero sentido contrario.

Vectores concurrentes

Son aquellos que sus líneas de acción se cortan entre sí, en un mismo punto.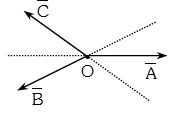

Se observa que las líneas de acción de los tres concurren en el punto “O”, por lo que son concurrentes

Operaciones con Vectores

Adición de Vectores

Al vector “suma” también se le llama resultante, la resultante produce el mismo efecto que los sumandos.

1. Método del Triángulo

Este método es sólo para dos vectores coplanares y concurrentes

Pasos a seguir:

• Se forma el triángulo, cuando son “SÓLO” 2 vectores
• Para hallar el valor de la resultante se aplica la Ley de Lamy o de senos:

2. Método del Paralelogramo

Pasos a seguir:

• La suma o resultante es la diagonal del paralelogramo formado.
• La suma o resultante se denota:

Analíticamente:

3. Método del Polígono

• Método del Polígono Abierto: Se usa generalmente para sumar más de dos vectores. Se colocan uno a continuación del otro, manteniendo constante su VALOR, DIRECCIÓN y SENTIDO. La resultante es el vector que parte del origen del primero y llega al extremo del último. Ejemplo:

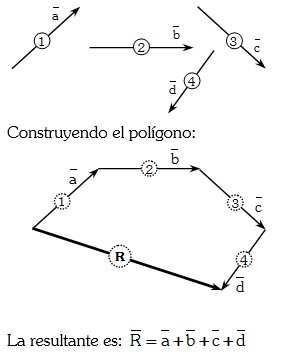
• Método del Polígono Cerrado: En este caso todos tienen la misma secuencia (horario). El extremo del último llega al origen del primero.

Diferencia de Vectores

La diferencia de vectores es llamada también resultante diferencia.

Casos Particulares y Posiciones Relativas de los Vectores

En los documentos que te dejaremos, encontraras 6 casos particulares y posiciones relativas de los vectores, te recomendamos verificar estos casos:

Descomposición Rectangular de un Vector

Aquí te mostramos como se da la descomposición rectangular de un vector:

Componentes rectangulares de un vector en el plano

Las componentes rectangulares están dadas por:

• Módulo del Vector A

• Dirección del Vector A Respecto al eje “X”

Vectores en el Espacio

Análogamente a los puntos del plano cartesiano que están representados por un par ordenado, los puntos del espacio se representan mediante ternas de números o coordenadas espaciales.

Puntos en el espacio

X: eje de abscisas, Y: eje de ordenadas, Z: eje de cotas

Expresión vectorial de un vector en el Espacio

Un vector A, se puede escribir como combinación lineal de sus vectores unitarios canónicos, así:

Dados dos puntos en el espacio, se puede hallar el vector que dichos puntos determinan, aplicando:

Módulo de un vector en el Espacio

El módulo de un vector “A”, está dado por:

Dirección de un vector en el Espacio

La dirección de un vector en el espacio, está dada por sus ángulos de orientación con respecto a los 3 ejes coordenados. Y a los cosenos de dichos ángulos se denominan cosenos directores.

Cosenos directores

Las direcciones del vector con respecto a los ejes coordenados están dados por:

Operaciones con Vectores en el Espacio

Suma y Diferencia de Vectores en el Espacio

Dados dos vectores:

Se define como vectores suma y diferencia, respectivamente:

Multiplicación por Escalar

Dado el vector “A” y un escalar “r” se define como producto por escalar a la operación:

Donde el vector rA, es múltiplo y necesariamente paralelo al vector A.

Propiedades de la Multiplicación por escalar:

Dado los vectores “A” y “B” y los escalares “r” y “s”, se cumple:

Producto Interno o Producto Punto

Dados dos vectores:

Se define como producto interno de vectores a la expresión dada por: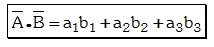

Observe que:

Otra definición:

Es posible también definir el producto interno mediante la relación:

Propiedades del Producto Interno:

Dado los vectores “A”, “B” y “C” y los escalares “r” y “s”, se cumple:

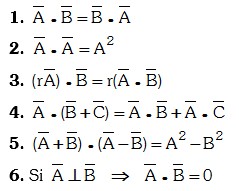
Importante:
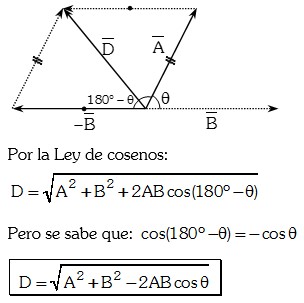
Del vector suma, de acuerdo a las propiedades:

Observe: ¡Esta es la ley del coseno!

Producto Vectorial o Producto Cruz

Dados dos vectores “A” y “B” se define como producto vectorial AxB, a la expresión definida por el determinante:

Propiedades del Producto Vectorial

Dado los vectores “A”, “B” y “C” y los escalares “r” y “s”, se cumple:

Producto de Vectores Canónicos

Puesto que un vector siempre es paralelo a sí mismo: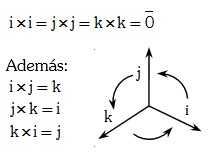

Regla de la mano derecha

Sirve para determinar la dirección del vector AxB

¡Observe!

Interpretación Geométrica del Vector AxB

El vector AxB, está representado por un vector perpendicular, tanto al vector “A” como al vector “B”. Su módulo es igual al área del paralelogramo formado.

Doble Producto Vectorial

Producto Triple

Dado los vectores “A”, “B” y “C”, se define como producto triple “A.(BxC)” a la expresión definida por un determinante de la forma:

Interpretación Geométrica de Producto Triple

El producto triple “A.(BxC)” de los vectores “A”, “B” y “C” es igual al volumen del paralelepípedo formado por dichos vectores.